Skip to content
Optigrid logo icon Optigrid
Pupillary distance statistics cover
Blog

What 14,904 Pupillary Distance Measurements Tell Us About Human Faces

Saulo Garcia
• 4 min read

Why look at PD at scale?

Pupillary distance (PD), the millimetres between the centres of your pupils, is the silent hero behind lens alignment. When PD is off, even a perfect prescription can feel blurry or induce strain. Because Optigrid captures PD remotely, we now have thousands of real-world readings instead of the handful an optician might see in a day. Analyzing them shows us interesting aspects of the human face and tells the truth without guesswork.

Our dataset in a nutshell

  • Source: Every PD captured by Optigrid between January and June 2025.
  • Sample size: 14904 unique sessions after scrubbing obviously invalid rows (see Methods note below).
  • Fields: Single binocular PD plus dual PD for left and right eyes.
  • Cleaning rules: Kept values in plausible adult ranges (40‑90 mm for single PD, 15‑50 mm per eye).

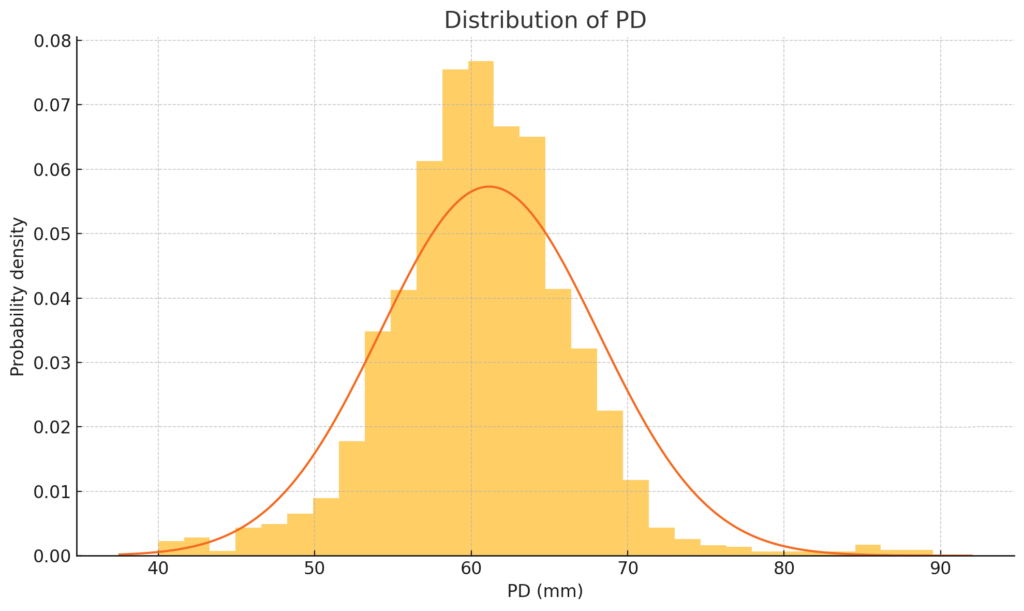
The bell curve in numbers

MetricSingle PD
Mean61.2 mm
Median60.6 mm
Standard deviation7.0 mm
5th–95th percentile51.5–71.1 mm
Maximum89.5 mm

The histogram fits a textbook normal curve with one curiosity: a small “second hump” beyond 80 mm that accounts for just under 1 % of users. We will revisit that in a moment.

Pupillary distance bell curve distribution across Optigrid users

Left and right eyes stay in lock‑step

Monocular PDs average 30.54 mm (left) and 30.57 mm (right). Their ratio to the single PD hovers at 0.50, and the summed dual PD agrees with the single PD within ±0.75 mm for 95 % of measurements. That tight symmetry signals that the algorithm is measuring, not guessing.

How do our numbers compare to the literature?

Published sources cluster adult PD around the low 60s. Warby Parker cites a typical range of 60‑64 mm, Zenni Optical gives 54‑74 mm, and the Cleveland Clinic pegs the average at 63 mm. (warbyparker.com, zennioptical.com, my.clevelandclinic.org)
Our mean of 61 mm and 5th‑to‑95th spread of 51‑71 mm fit snugly inside those brackets. In other words, our remote tool is mapping the same population curve traditional clinics see.

The story behind the high‑right tail

Why do 104 people register PDs of 80 mm or more?

  1. Big heads are real. Anthropometry studies put the tallest 2‑3 % of males above 78 mm.
  2. Scale drift. If the reference card tilts forward, its apparent width shrinks and every distance inflates by the same factor. Because dual PD tracks single PD precisely in this cluster, scale drift is a likely co‑conspirator.

We are adding a card‑angle check so future posts can separate biological giants from geometric artefacts.

Why it matters for online eyewear

  • Lens accuracy: Sub-millimetre PD error keeps prism within ISO tolerances, reducing returns.
  • Frame recommendations: Knowing that half the audience sits between 58‑64 mm lets us tailor which SKUs appear first.
  • UX prompts: Only 1 in 60 users produce an extreme PD, so nudging just that slice to re‑capture keeps friction low for everyone else.

What’s next

Our next data drop will cross‑reference PD with self‑reported country to see if regional genetics show up. We will also slice by other dimensions. Male users have on average higher PD measurements, but for privacy reasons, we can’t tag that information in the measurement data.

Methods note

Full cleaning and analysis recipe (Python + pandas). It loads the CSV, coerces numeric types, applies range filters, and overlays a normal probability density on a 30‑bin histogram.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from ace_tools import display_dataframe_to_user

# 1. Load the raw file
df = pd.read_csv('./optigrid_production_20250630_171750.csv',
                 header=None,
                 names=['PD', 'PD_L', 'PD_R'])

# 2. Convert to numeric and drop obviously invalid (non‑numeric / NaNs / ±inf)
df = df.apply(pd.to_numeric, errors='coerce')
df = df.replace([np.inf, -np.inf], np.nan).dropna()

# 3. Simple physiological range filter to cull extreme outliers
outlier_mask = (
    (df['PD'] < 40) | (df['PD'] > 90) |   # monocular PD usually 50‑75 mm
    (df['PD_L'] < 15) | (df['PD_L'] > 50) |
    (df['PD_R'] < 15) | (df['PD_R'] > 50)
)
df_final = df[~outlier_mask].copy()

# 4. Extra derived columns for deeper inspection
df_final['PD_sumLR'] = df_final['PD_L'] + df_final['PD_R']
df_final['PD_diff'] = df_final['PD'] - df_final['PD_sumLR']

# 5. Descriptive statistics table
summary = df_final[['PD', 'PD_L', 'PD_R', 'PD_diff']].describe().T.round(2)
display_dataframe_to_user("Cleaned PD Summary", summary)

# 6. Bell‑curve style histograms with overlaid normal PDF
for column in ['PD', 'PD_L', 'PD_R']:
    data = df_final[column]
    mean = data.mean()
    std = data.std()
    
    plt.figure()
    plt.hist(data, bins=30, density=True, alpha=0.6)
    
    # overlay the theoretical normal curve
    xmin, xmax = plt.xlim()
    x = np.linspace(xmin, xmax, 400)
    pdf = (1 / (std * np.sqrt(2 * np.pi))) * np.exp(-((x - mean) ** 2) / (2 * std ** 2))
    plt.plot(x, pdf)
    
    plt.title(f"Distribution of {column}")
    plt.xlabel(f"{column} (mm)")
    plt.ylabel("Probability density")
    plt.tight_layout()
    plt.show()

Blog