Minimum Blank Size (MBS) Calculator: A Quick Formula & Explanation
This post presents the common method for estimating the minimum lens block diameter, also known as Minimum Blank Size (MBS), using the formula “Frame Bridge + Frame Width – PD + Longest Diagonal + 2 mm” widely adopted in labs and optical shops. Despite its simplicity, this method offers bench‑speed calculation and a safety margin for block cutting, but it may introduce inaccuracies for complex frame geometries
🛠️ Lens Diameter Calculator (MBS Calculator)
To get an approximate block diameter:
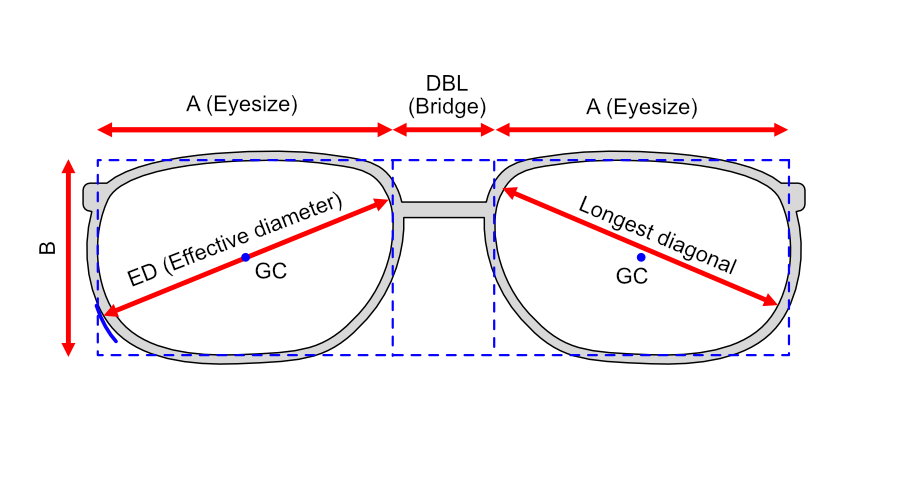
- A – inner horizontal width of the frame eye
- Bridge (DBL) – distance between lenses at the nasal bridge
- PD – twice the smaller interpupillary nasal distance (2× Smallest Dual PD)
- ED – Effective diameter (In some cases, the lon)

Approximate Lens Diameter Formula
MBS ≈ Bridge (DBL) + A – PD + ED + 2 mmWhy this formula?
- Quick at the workbench: avoids full geometric calculations or decentration math
- Built-in safety margin: the “+ 2 mm” provides extra allowance for finishing and fitting variations
- Minimal tools needed: only a ruler and pupilometer – no digital tracer required
Effective Diameter vs Longest Diagonal
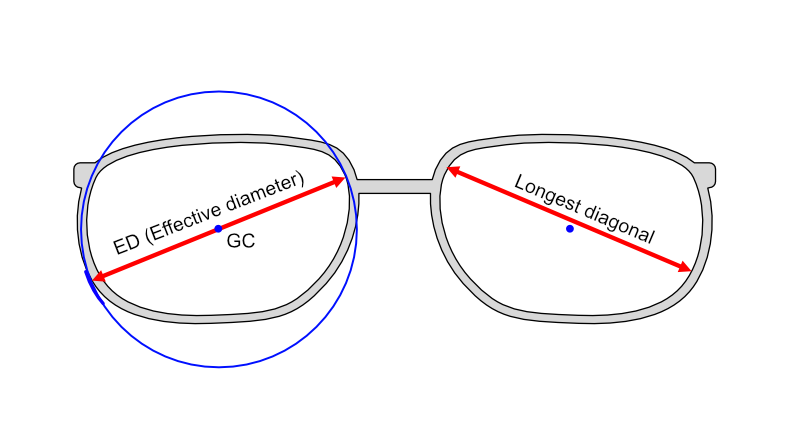
The effective diameter (ED) is the most precise measurement for the lens block, but it’s harder to measure manually
Therefore, the longest diagonal (DM) is used as a proxy – with the additional “+ 2 mm” margin to compensate for under‑measurement
Formula Parameters: What Each Term Means
- Bridge (DBL): The smallest distance between the eyeglass frames at the nose.
- Frame Width (A): The inner horizontal width of the frame eye.
- PD (2 × smaller PD): Optical centration uses the PD of each eye, multiplied by two.
- Effective Diameter (ED): The biggest distance between the geometric center of the lens and the edge of the frame eye TIMES 2
- Safety Margin (+ 2 mm): Added – sometimes 3 mm – to ensure the block isn’t too tight
Risks of the Quick Approximation
- Inaccuracy in asymmetrical frames (e.g. cat-eye, aviator, frames with notches)—these may require an ED larger than the formula suggests
- Material waste: excessive waste in standard frames can increase thickness and cost
- Optical prism errors: using total PD instead of on-an-eye PD can induce unwanted prism
- Not suitable for free‑form digital labs: these labs typically calculate ED exactly (2× radius), without fixed extra margins
- Not suitable for progressive lens: This method does not take into account the segment height and the vertical decentration
Advantages & Best Practices
- Speed at the counter: no need for digital tracer, enabling order completion in seconds
- Easy setup across any optical shop: all required tools (rulers and pupilometers) are commonly available
- Compatible with online tools: calculators like OptiCampus and Chadwick Optical support this approximation method
- Efficient for batch production: well‑suited for manufacturing conventional bifocal and progressive lenses.
Equivalent Formula Using Effective Diameter & Decentration
MBS = ED + (2 × Decentration)Understanding Decentration:
Decentration is the horizontal offset between the geometrical center of the frame eye (lens shape) and the patient’s pupil center (Single eye DP)
Decentr = (GCD ÷ 2) – Single Eye PD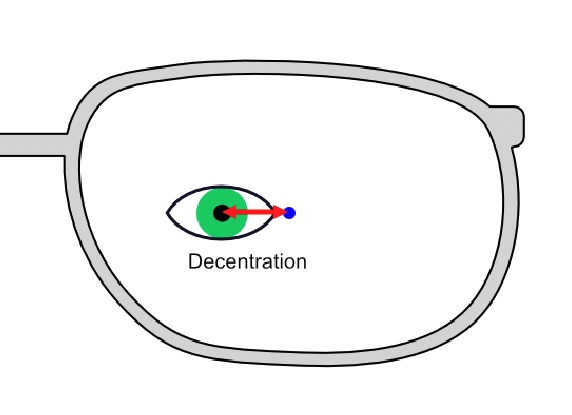
This way, you can calculate MBS separately for each eye
How Optigrid Enhances Accuracy
Optigrid goes beyond approximation:
- Computes the actual Effective Diameter (ED) by analyzing a patient’s photo and the frame outline
- Eliminates fixed margins, ensuring the smallest possible block size without compromising quality
TL;DR Summary
| Concept | Standard Formula | Optigrid’s Methodology |
|---|---|---|
| Speed & tools | Instant, manual (ruler + pupilometer) | Automatic, based on image and frame design |
| Accuracy | Approximate, +2 mm overcompensation | Exact ED + calculated decentration |
| Use case | Simple shop workflows, standard frame shapes | Custom shapes, asymmetrical frames, free‑form production |
| Risk of prism or wastage | Medium | Low |
Conclusion
This widely used rule of thumb “Bridge + Frame Width – PD + Diagonal + 2 mm” offers a fast and accessible block‑sizing solution. However, it comes with limitations in accuracy, especially for asymmetrical or complex eye shapes.
Optigrid, on the other hand, automates the process, using real ED measurements and decentration data extracted from images to compute the minimum required block size, optimizing lens material and reducing errors in layout.